An Introduction To Tries

I will describe tries and explain why they are so important.
Introduction
Tries are used extensively in blockchain systems and elsewhere. They are tree structures that represent sets of key value pairs in software. It is possible to instead just represent key value pairs contiguously. However, then it would be more difficult to make changes and perform searches than with tries. Tries are composed of connected nodes that store values. Different nodes imply different keys based on their positions. A common application that uses tries is internet routing.
Examples
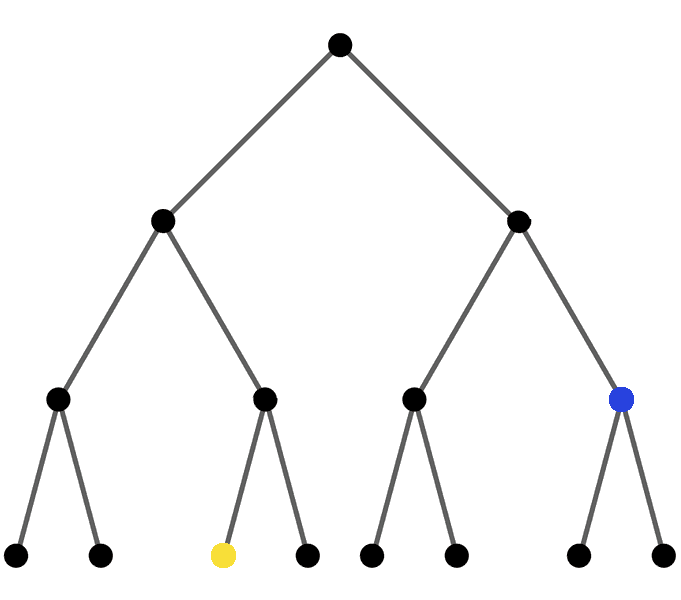
In the trie diagram above, the dots represent nodes and line segments represent connections. Note that each dot has a left and right line segment below it. The key corresponding to each node is found as follows:
- Find the path from the top node to the node.
- For each left line segment along the path, add a "0" to the key.
- For each right line segment along the path, add a "1" to the key.
Therefore, the yellow dot corresponds to the key "010". The blue dot corresponds to the key "11". A similar procedure is used for all tries to determine keys.
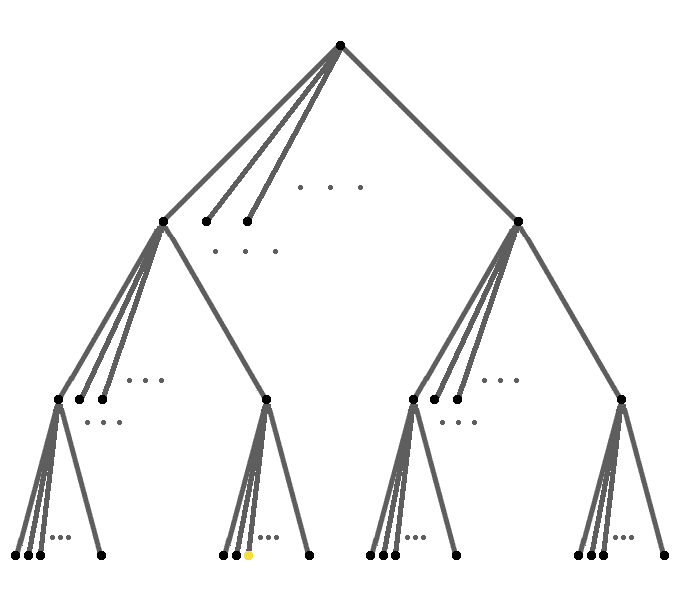
The diagram above represents a trie where each node connects to 16 nodes below it. Note that each line segment will add one of 16 possible values (nibbles) to the keys. Therefore, the yellow dot corresponds to the key with the hexadecimal representation "0x0f2". The previous trie diagram represented 15 nodes. This one represents 4369 nodes!
Compression

When representing sets of key value pairs with tries, there is often thousands of unused nodes. Compression techniques are often used to more efficiently store tries with lots of unused nodes.
Nomenclature

The terms radix trees and Patricia trees also refer to tries. Sometimes, but not always, these terms imply "compressed" tries that more efficiently manage unused nodes.
Conclusion

Tries are tree structures that store key value pairs in a format that facilitates changes and searches. They are used extensively in many applications. Hopefully now you have gained the fundamentals to be able to take a deeper dive into these concepts.
Feedback
You can contact me by clicking any of these icons:



Acknowledgements
I would like to thank IOHK (Input Output Hong Kong) for funding this effort.
License
This work is licensed under the Creative Commons Attribution ShareAlike 4.0 International License.
