Cuban Piracy & Why Merkle Trees Are So Awesome For Blockchains

October 12, 2016

Christian Seberino

I will explain Merkle trees and why they are so important for blockchain systems.

Introduction

The sending of information today is horrendously slow compared to the processing of information. Therefore, when distributing information on a peer to peer network, it is desirable to minimize communications even if that implies adding computations. Hashes can help confirm the integrity of information with minimal communication. Hash trees, or Merkle trees, can also help identify invalid bits with minimal communication.

El Paquete Semanal

To understand the importance of Merkle trees for blockchains, consider El Paquete Semanal ("the Weekly Package"), part of one of the strangest peer to peer networks in the world. Every week a terabyte of YouTube videos, pop music MP3s, Spanish news articles and more is distributed to Cubans for a few pesos. Distribution sometimes depends on such methods as passing hard drives around by hand. This is because connectivity in Cuba is so poor. 95% of homes have none, and, the remaining 5% are subject to strong censorship. Suppose you wanted to give everyone a perfect copy of El Paquete Semanal. Because of the slowness of the network, it is impractical to resend copies to correct errors. How would you quickly find and fix errors without resending many bits? That is where Merkle trees come in.

Fast Search

To understand why Merkle trees can be used to find errors so efficiently, try this activity: Have a friend pick any city in any part of the world. Google Maps might be helpful. Start asking yes / no questions to determine the city. You might ask questions like, "Is the city above or below the equator?", and, "Is it to the east or west of Cairo?". You should notice that cutting the search space approximately in half every question leads to the answer amazingly fast. Merkle trees allow a similarly fast search.

Merkle Trees

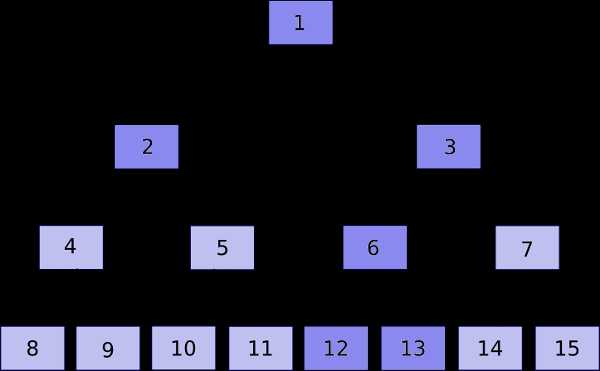
Here is a Merkle tree recipe to quickly find corrupted segments in El Paquete Semanal:

Split it into eight segments and hash those segments. In the figure above, those eight hashes are represented by the boxes labelled 8 through 15. Then, hash consecutive pairs of those hashes. These are represented by the boxes labelled 4 through 7. Hash consecutive pairs of this second set of hashes as well. These are represented by the boxes labelled 2 and 3. Finally, hash these last two hashes. This is represented by the box labelled 1. Refer to the hash corresponding to label 1 as hash 1, the hash corresponding to label 2 as hash 2, etc.

Check hash 1 to determine if there are any errors to fix or not. Suppose the segment associated with hash 13 is corrupt. Check hashes 2 and 3 to determine the erroneous segment is associated with hash 6 or 7. Then, check hashes 6 and 7 to determine the bad segment is associated with hash 12 or 13. Finally, check hashes 12 and 13 to determine the faulty segment is associated with hash 13. Smaller segments would require a similar process with more levels to the Merkle tree.

For many small segments (lots of levels), using a Merkle tree to check and fix a remote copy requires much less communication than sending all the hashes of all the segments. It minimizes communications at the expense of some extra hash calculations.